Blk - Cálculos con bloques

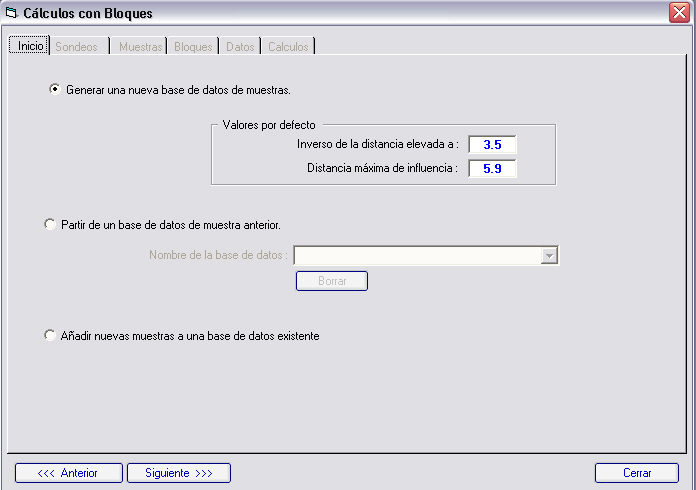
En la opción de cálculos con bloques se pueden calcular las leyes y litologías de los bloques mediante interpolación con la información de las muestras de un grupo de sondeos.

En la primera subcarpeta tendremos tres opciones:

• Generar una nueva base de datos de muestras: para ello le daremos la potencia para los cálculos por el inverso de la distancia y la máxima distancia de influencia de las muestras, al pasar a las siguientes subcarpetas podremos seleccionar los sondeos de los cuales leerá las muestras para el cálculo.
• Partir de una base de datos de muestras anterior: para lo cual nos saldrá una lista de las generadas en otros cálculos. Si elegimos esta opción, pasará luego directamente a la subcarpeta de muestras. Aquí tenemos también la opción de borrar bases de datos de muestras que ya no utilicemos pulsando en el botón borrar.
• Añadir nuevas muestras a una base de datos existente: en este caso debemos de seleccionar la base de datos a la cual añadirá las muestras de los sondeos que seleccionemos en la siguiente subcarpeta.

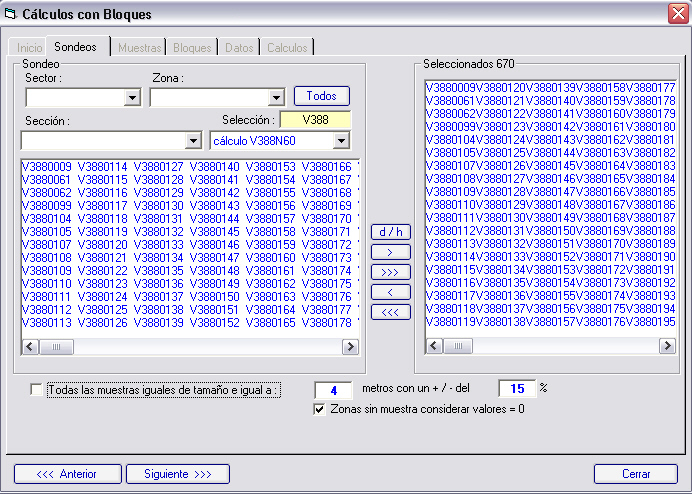
En la subcarpeta sondeos seleccionaremos los sondeos que contienen las muestras para el cálculo. Tendremos también la opción de recomponer las muestras con un ancho dado, pues las muestras deben de tener un tamaño parecido al tamaño medio del bloque, o sea para calcular leyes de bloques de 4x4x4, lo normal es que las muestras se redefinan con tamaño de 4 metros.

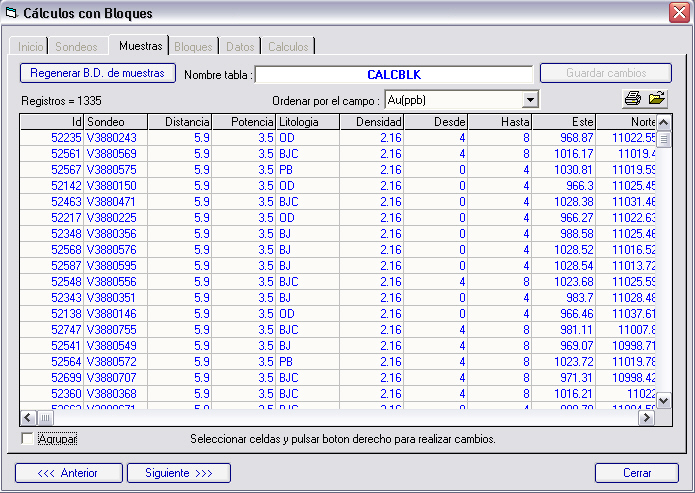
En la subcarpeta muestras tendremos todas las muestras para el cálculo, con las posiciones del centro de cada una para la interpolación.

En este apartado podemos modificar los datos de la tabla seleccionando las celdas que queramos cambiar y pulsando el botón derecho del ratón; así por ejemplo podemos reducir la distancia de influencia de algunas muestras, etc.

Podemos ocultar o mostrar columnas pulsando con el ratón sobre la cabecera.

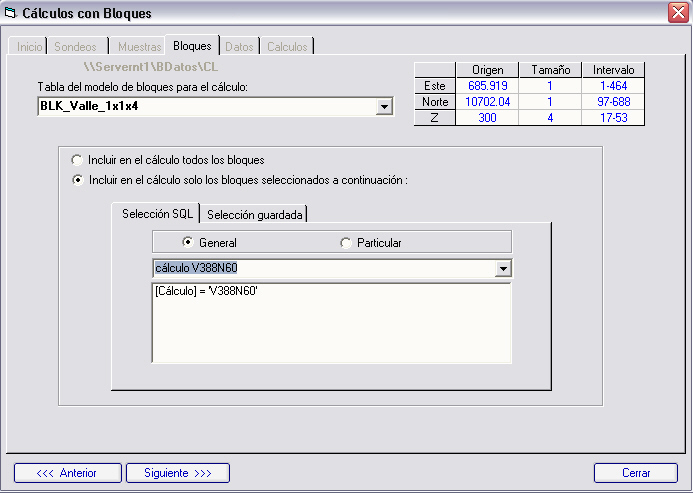
En la siguiente subcarpeta llamada bloques, seleccionaremos los bloques de la base de datos que van a ser recalculados. El proceso de selección es el mismo que el programa utiliza en otros módulos, bien por SQL o por selección guardada en el módulo de dibujo.

En la subcarpeta datos incluiremos la información necesaria para los cálculos. Podemos realizar:

• Cálculo de litologías (campos alfanuméricos), para los cual el programa utilizará el método del más cercano, o sea la muestra que está más cerca (según el elipsoide de búsqueda) del centro del bloque será la que le dé la litología a ese bloque. Tendremos la opción de recalcular el campo peso utilizando para ello la densidad de esa litología que tenemos en el índice de litologías de los sondeos.

• Cálculo de leyes (campos numéricos), para este caso podemos elegir entre el cálculo por el inverso de la distancia elevado a una potencia, el inverso de la distancia mas una constante elevado a una potencia o el mas cercano.

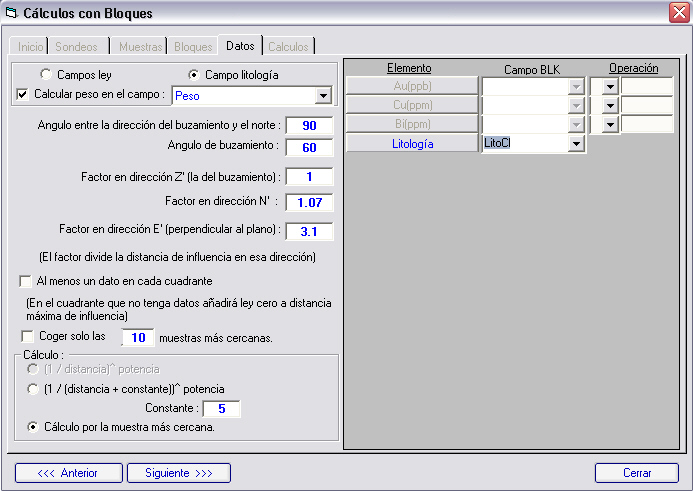
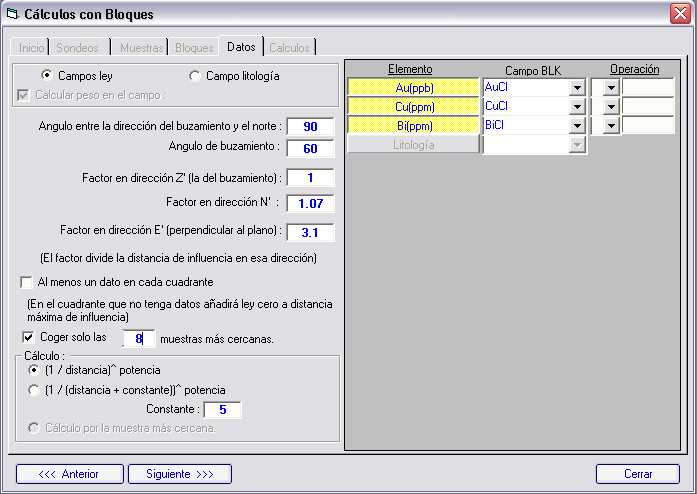
Según el tipo de cálculo podremos seleccionar unos elementos de las muestras y los correspondientes que van a ser calculados para los bloques, y si lo deseamos podemos hacer que tras el cálculo se guarde en otra unidad añadiendo una operación como puede ser la de dividir por 1000 si queremos pasar de ppb a ppm por ejemplo.

Podemos además definir un elipsoide de búsqueda, el cual estará definido por un plano principal, introduciendo el azimut de la línea de máxima pendiente de ese plano, que será el eje principal (dirección Z') y el buzamiento, el eje perpendicular al principal en el plano será el secundario (en dirección N') y el perpendicular al plano el terciario (dirección E'). Introduciendo factores de división en los tres ejes, definiremos el elipsoide, si los tres son la unidad, será una esfera y no habrá reducción de distancias. Si el factor en el eje principal es la unidad y en el eje N' es 2, significa que una muestra que esta a 10 metros de distancia en el eje principal (Z'), tiene la misma influencia en el cálculo que una que esté a 10/2=5 metros en el eje N'.

Podremos además limitar el número de muestras máximo que entran en el cálculo y obligar a que tenga al menos un dato en cada uno de los ocho cuadrantes, añadiendo un dato de cero a distancia de máxima influencia en el caso de no tener datos en ese cuadrante.

En la subcarpeta cálculos podremos iniciar el proceso, pararlo y selecionar que nos guarde la información intermedia en un fichero TXT para su verificación.